II - La parabole
En mathématiques il existe les coniques ou sections coniques , (trouve par Apollonius de Perge , au IIIe siecle av.JC)c'est l'intersection d'un cone et d'un plan ne passant pas par son sommet.
Le terme de sections coniques est pour désigner ses courbes, c’est depuis simplifier en coniques. Si le plan rencontre les deux napes du cone ou une seul on obtient donc une hyperbol ou une éllipse et dans le cas intermédiaire, une parabole. Pour mieu comprendre ce phénomène voici trois schéma représentatif :
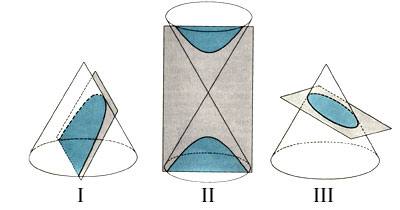
Sur le schéma numéro I: nous pouvons voir qu'ici le plan coupe les deux nappes d'un cone,ce qui nous donnes une ellipse.(?)
Sur le schéma numéro II :nous remarquons que le plan coupe une nappe d'un cone,ce qui nous donnes une parabole.(?)
Sur le schéma numéro III: nous constatons que le plan rencontre les deux nappes d'un cone alors c'est une hyperbole.(?)
Les coniques se distinguent donc selon qu'elles sont bornéees ( ellipse), non bornées a une seule branche ( parabole) ou a deux branches (hyperbole).Il est dit que les ellipse et les hyperbole sont des « coniques a centre » car elles ont un centre de symétrie.Elles ont également deux axes de symétrie orthogonaux entre eux ,alors que la parabole ,elle, n'en a qu'un .Une ellipse désigne une omission c'est à dire un manque.Ansi,en géométrie,il s'agit d'un cercle raté.Parabole signifie « jeter à coté »,d'où « comparer ».L'origine du therme mathématiques est liée à la construction de la parabole comme un lieu des points équidistants d'un point et d'une droite,autrement dit,on compare deux distances. Voici un shéma permettant de mieux comprendre
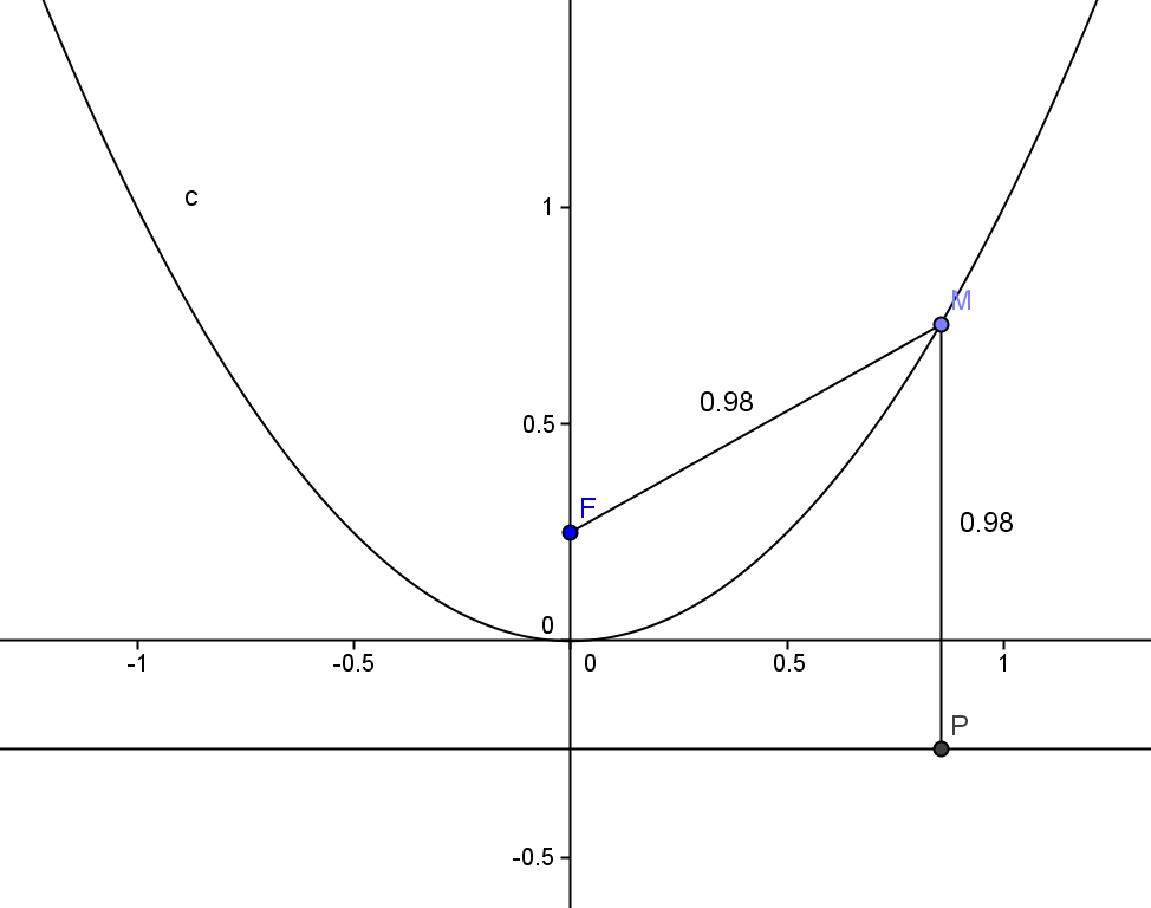
Explication de construction de la parabole ,ci-jointe :
-On connait la parabole d'équation y = x²
-Faire cette parabole
-Démontrons que MF et MP sont égaux.
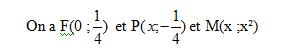
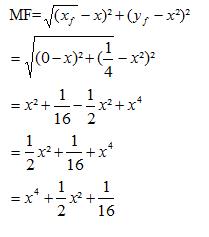
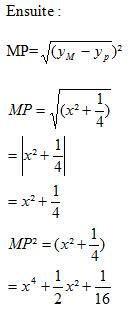
On remarque que MP et MF sont égaux.
Alors alors cela vérifie la propriété de la parabole.
Pourquoi la parabole ?
La parabole est un outil mathématiques qui nous intéresse puisqu'elle détient des propriétés propre au miroir parabolique. Alors, ce miroir parabolique, utilise
les propriété de la parabole pour réfléchir les rayons lumineux en un seul point, le foyer (F). C'est donc là que les lois de réfléxions de Snell Descartes interviennent.